SÉRIE
|
TURMA
|
TURNO
|
1 °
|
A e B
|
TARDE
|
CONTEÚDO
Função afim: conceito, lei de formação, gráfico e
aplicações.
|
||
DESCRITOR
28 ,44 ,75
|
||
OBJETIVO
ü Expressar a dependência de uma variável em relação à outra.
ü Construir o
gráfico de uma função afim a partir da lei de associação.
ü Determinar a lei
de associação a partir do gráfico.
ü Dar exemplos de
funções afim no cotidiano.
|
||
ROTEIRO DE TRABALHO
Atividade 1 – Apresentação de situações problemas que
envolvem leitura e representação de gráficos no plano cartesiano e equações
de 1º grau para sondar de quais conhecimentos a turma dispõe.
Atividade 1.1 – Experimento matemático, mostrando a
relação direta existente entre o número de bolinhas de gude e o nível de água
numa proveta graduada, em seguida construir tabelas e perceber as
dependências de uma variável em relação a outra, determinar uma lei de
associação e expressar no gráfico o comportamento dos valores das grandezas.
Atividade 1.2 – Aprimorar o conteúdo, reconhecendo onde e
quando a função afim aparece no cotidiano, por meio de pesquisas no comércio
local e dentro da própria escola.
|
||
RECURSOS
Calculadoras, papel quadriculado, bolinhas de gude, provetas
graduadas, livro didático.
|
||
Avaliação
Será Contínua durante todo processo, o aluno será observado quanto a
sua participação nas atividades desenvolvidas em sala ou fora dela, Trabalhos
em grupos apresentando diversas funções e que os alunos reconheçam
se elas são afim sem construir os gráficos, justificando a resposta. Depois,
sugerir que eles montem os gráficos na
folha quadriculada para verificar se o que pensam faz sentido.
|
||
Matemática e Prática
segunda-feira, 11 de agosto de 2014
O jeito mais fácil e certo de aprender Função afim
Mais uma ação do PJF da EEM Professora Marieta Santos, atividades práticas envolvendo um dos conteúdos mais importante do 1° ano do ensino médio , Função Afim .O melhor caminho é estimular os alunos a pensarem nas relações que existem entre variáveis, buscar a regularidade entre elas e daí estabelecer a generalização para a situação.
quarta-feira, 21 de maio de 2014
|
segunda-feira, 19 de maio de 2014
CONCURSO DE FRASES USANDO SINAIS MATEMÁTICOS
Introdução
Ao longo dos anos, a Matemática tem se
aprimorado de forma a facilitar os cálculos e a compreensão dos colaboradores,
os símbolos deixam-na cada vez mais dinâmica e aplicável no contexto do
cotidiano. A lógica tem o papel de formalizar e deixar mais simples os
cálculos, no intuito de universalizar os estudos e o próprio ensino da
Matemática. Os símbolos foram surgindo e sendo introduzidos com a evolução da
forma de pensar e raciocinar do homem, do surgimento de cálculos complexos, da
aplicação nas diversas ciências em que a Matemática contribui, na
fundamentalização de situações práticas.
Em razão do incessante interesse do homem em criar, inventar, reinventar, aprimorar, a Matemática tem se tornado uma ferramenta de grande importância na evolução da sociedade
Em razão do incessante interesse do homem em criar, inventar, reinventar, aprimorar, a Matemática tem se tornado uma ferramenta de grande importância na evolução da sociedade
JUSTIFICATICA
Considerando-se a importância da linguagem matemática e os
significados de seus sinais para interpretar e resolver situações problemas, é
que o professor de matemática da EEM Marieta Santos ,Vagner Matos, propõe a
seguinte ação.
OBJETIVO GERAL
Criar oportunidade para motivar e incentivar o corpo
discente da importância da matemática e o uso de sinais para interpretar e resolver situações
problemas, auxiliando no processo ensino aprendizado através de atividades dinâmicas.
OBJETIVO ESPEFÍCO
ü
Reconhecer os sinais matemáticos para resolver
problemas
ü
Desenvolver a leitura, interpretação a partir de
estudo de sinais matemáticos.
ü
Desenvolver a criatividade em criar frases
usando símbolos e sinais matemáticos
METODOLOGIA
ü
Exposição os símbolos matemático para os alunos;
ü
Criação
de frases utilizando os símbolos matemáticos;
ü
Confecção
de cartazes com as frases;
ü
Exposição
de cartazes nas galerias do Colégio
ü
Concurso de frases criativas usando sinais
matemáticos;
ü
Premiação da frase mais criativa.
CRONOGRAMA
DATA
|
ATIVIDADE REALIZADA
|
RESPONSÁVEIS
|
30/04/14
|
Apresentação do projeto aos alunos, gestores e Professores
|
Prof Vagner matos
|
02/05/14
|
Confecção das frases nas aulas de Matemática
|
Prof Vagner Matos
|
08/05/14
|
Exposição de cartazes e
escolha da frase mais criativa
|
Professores e Gestores
|
08/05/14
|
Premiação dos alunos que tiveram as frases.
|
Professores e Gestores
|
AVALIAÇÃO
Serão avaliados a participação, a criatividade e o
desempenho dos alunos na atividade de produção das frases usando sinais
matemáticos.
“Multiplicar a cidadania,
subtrair a diferença”. X a cidadania , - a ≠A fórmula para um mundo melhor é simples. Pratique-a.
Aqui estão as frases criadas pelos alunos:
Aqui estão as frases criadas pelos alunos:
2° ANO B TARDE
HÁ UMA ∆ ENTRE AMAR
E GOSTAR .GOSTO DE TODOS + AMO SÓ VOCÊ.
VOCÊ É = A ∑ DE TODA A BELEZA QUE ∃
MEU MUNDO É
UM ∅ SEM VOCÊ
TALITA DOS SANTOS ARAÚJO
NOSSA ∪ É IGUAL ∀ COISA
SE VOCÊ DEIXAR POSSO
OCUPAR O ∅ QUE ∃ EM SEU CORAÇÃO
A ∪ É IGAUL A √ QUE
SUSTENTA UMA AMIZADE VERDADEIRA
AMAR É A √ DA FELICIDADE E A X DO ∞
A VITÓRIA É ≫QUE O FRACASSO, ∴ ∄
NADA IMPOSSÍVEL. SÓ ∃
PESSOAS INCAPAZES DE FAZER DO FRACASSO UM ℤ CAMPEÃO.
ANDREIA MARIA
Camila Felipe
quarta-feira, 14 de maio de 2014
Atividade Pedagógica
Metodologia Entre Jovens Matemática - 9 º ano do Ensino Fundamental / 1 º ano do Ensino Médio
Elaboração de plano de hum Parágrafo o Desenvolvimento de UMA oficina.
1. Serviços Tema trabalhado hum.
2. Descritor (es).
3. Objetivos da oficina.
4. Roteiro de Trabalho da oficina.
5. Atividades propostas.
6. Recursos Que Serao utilizados Para O Desenvolvimento Das Atividades.
7. Ano do Ensino Medio / turma Opaco realizará Como Atividades da oficina.
8. Forma (s) de avaliação.
SÉRIE
|
TURMA
|
TURNO
|
1 °
|
A
|
TARDE
|
TEMA
Regra de Três e Porcentagem
|
||
DESCRITOR
D28-Resolver Problema Que porcentagem envolva.
|
||
OBJETIVO
Calcular porcentagem usando Regra de Três POR Meio de Atividade lúdica.
|
||
ROTEIRO DE TRABALHO
Atividade 1 - Aulas expositiva dialogada COM USO de Materiais COM folhetos Comerciais COM porcentagens, Jornais e OUTROS, Fazendo o Aluno perceber a importancia do Conhecimento sobre porcentagem na Vida Cotidiana.
Atividade 1.1 - Situações Problemas resolvidas los Grupos, envolvendo Cálculos de Porcentagem utilizando Regra de Três na resolução.
Atividade 1.2 - aprimorando o Conteúdo Regra de Três e Porcentagem POR Meio de Atividade
lúdica (Jogo: Das Tabuleiro porcentagens) Joe Cada Grupo na SUA Vez joga 2 Dados, efetua OS Cálculos necessários e Colocasia o Seu marcador Localidade: Não tabuleiro. Ganha o Jogo QUEM conseguir marcar Primeiro Toda a Tabela.
|
||
RECURSOS
Calculadoras e Notícias de Jornais, Propagandas e folhetos Comerciais COM porcentagens, Jogo de tabuleiro Das porcentagens (dados, Marcadores e Tabelas)
|
||
Avaliação
Sera, Contínua Durante TODO O Processo. O Aluno Sera, Sera, Sera observado Quanto a SUA Participação NAS Atividades desenvolvidas los SALA, Em Casa, Trabalhos los Grupos, Superdownloads e Desafios empre Grupos COM Calculo porcentagens de Mentais. Uma prova com questões formais Opaco propiciem AO Aluno resolver e identificar com porcentagens aprendidas Como Estratégias.
|
||
quinta-feira, 13 de fevereiro de 2014
strutura Curricular
PROF : VAGNER MATTOS
EEM PROF MARIETA SANTOS
| MODALIDADE / NÍVEL DE ENSINO | COMPONENTE CURRICULAR | TEMA |
|---|---|---|
| Ensino Fundamental e Médio | Matemática | Espaço e forma |
Dados fhghgAula
O que o aluno poderá aprender com esta aula
O aluno irá vivenciar atividade concreta que envolve o Teorema de Pitágoras.
Duração das atividades
Uma aula de 50 minutos.
Conhecimentos prévios trabalhados pelo professor com o aluno
Triângulos.
Quadrados.
Áreas.
Teorema de Pitágoras.
Quadrados.
Áreas.
Teorema de Pitágoras.
Estratégias e recursos da aula
Objetivo desta aula:O Objetivo desta aula é propor alguns objetos de aprendizagem que permitam um contato diferenciado com o Teorema de Pitágoras. Vale ressaltar que a proposta é diferenciar a dinâmica de aula, isso inclui materiais concretos, objetos virtuais e, também, atividades tradicionais como, por exemplo, a demonstração do Teorema.
Primeira Atividade: Material Concreto
Materiais necessários:
Cada aluno deve ter uma folha com o xerox da seguinte figura:
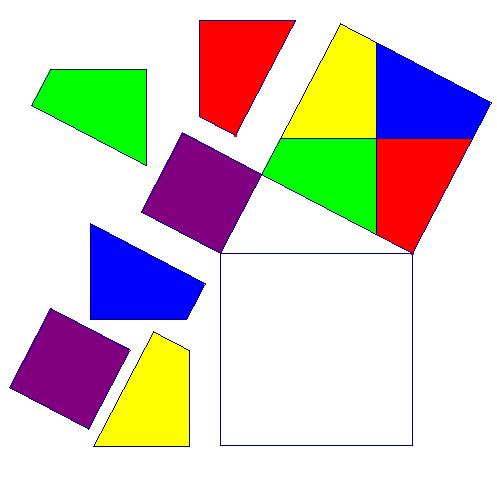
Sugestão:
Imprimir junto, para distribuir aos alunos, uma orientação da atividade:
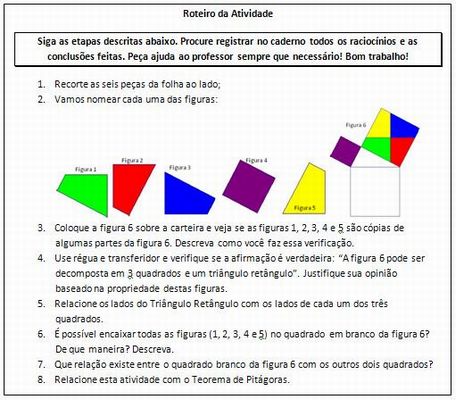
Professor, se este xerox for em preto e branco, verifique se é possível distingüir os diferentes polígonos no xerox. Vale observar que é possível colocar duas destas figuras em cada folha de papel A4. Ou então, uma figura e um roteiro.
Os alunos também devem ter tesoura, régua e transferidor.
Proposta da Atividade:
A vantagem de se usar o material concreto é a possibilidade de sobrepor figuras e observar que elas são congruentes.
Explore, ainda, que:
Neste momento, acontece a conclusão:
Como a peça 4 tinha área b2 e as peças 1, 2 3 e 5, juntas, tinham área c2 e todas conseguiram completar, sem perda nem sobra de espaço, a área do terceiro quadrado que é a2, então, temos: a2=b2+c2. A mesma informação tinha correspondência ao triângulo retângulo, logo, podemos interpretá-la como: "No triângulo retângulo a medida da hipotenusa ao quadrado é igual à soma dos quadrados dos catetos" - Teorema de Pitágoras.
Primeira Atividade: Material Concreto
Materiais necessários:
Cada aluno deve ter uma folha com o xerox da seguinte figura:
Sugestão:
Imprimir junto, para distribuir aos alunos, uma orientação da atividade:

Professor, se este xerox for em preto e branco, verifique se é possível distingüir os diferentes polígonos no xerox. Vale observar que é possível colocar duas destas figuras em cada folha de papel A4. Ou então, uma figura e um roteiro.
Os alunos também devem ter tesoura, régua e transferidor.
Proposta da Atividade:
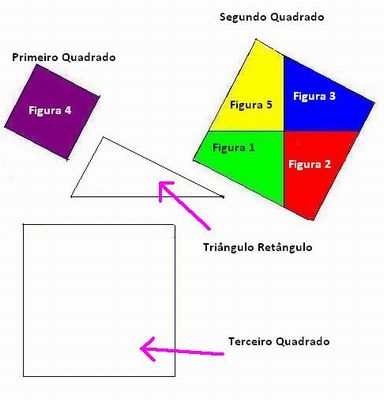
- Observação da figura: Peça para que os alunos recortem as seis peças da figura. Veja abaixo quais são para orientá-los.

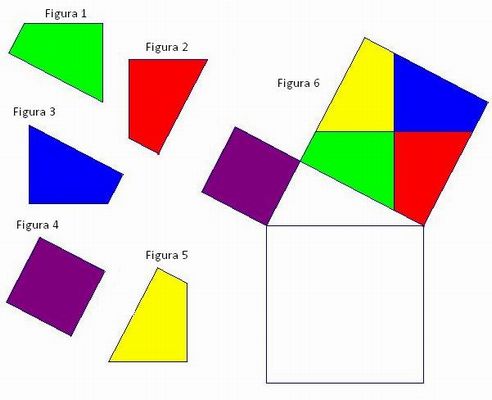
- Interpretação da figura: Os alunos devem fazer uma comparação de áreas das figuras 1, 2, 3, 4 e 5 com a figura 6. O objetivo desta atividade é que eles percebam que o polígono se encaixa (por sobreposição) em uma parte da figura 6 que tenha a mesma cor. Assim, os alunos encontrarão a seguinte figura:

A vantagem de se usar o material concreto é a possibilidade de sobrepor figuras e observar que elas são congruentes.
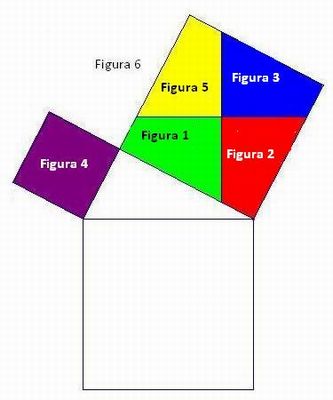
- Conhecendo a figura 6: Utilizando uma régua e transferidor, os alunos podem constatar que a figura 6 é composta de três quadrados (Primeiro quadrado: Figura 4; Segundo quadrado: União das figuras 1,2, 3 e 5; e um Terceiro quadrado que se encontra em branco) e um triângulo retângulo como na figura abaixo:

Explore, ainda, que:
- Existe um lado que é comum ao triângulo retângulo e ao primeiro quadrado. Se chamarmos a medida desta intersecção de "b" podemos concluir que um dos catetos do triângulo retângulo mede "b" e o lado do primeiro quadrado também mede "b". Logo, a área do primeiro quadrado será "b2".
- Também temos um lado que é comum ao triângulo retângulo e ao segundo quadrado. Se chamarmos a medida desta intersecção de "c" podemos concluir que o outro cateto do triângulo retângulo mede "c" e o lado do segundo quadrado também medirá "c". Logo, a área do segundo quadrado será "c2".
- Ainda temos um lado que é comum ao triângulo retângulo e ao terceiro quadrado. Se chamarmos a medida desta intersecção de "a" podemos concluir que a hipotenusa do triângulo retângulo mede " a" e o lado do terceiro quadrado também me de "a". Logo, a área do primeiro quadrado será " a2".
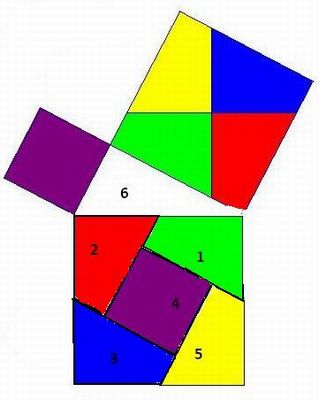
- Conclusão: Após toda esta exploração, é necessário voltar à mesa com as seis figuras novamente separadas. Pergunte aos alunos se é possível encaixar as peças 1, 2, 3, 4 e 5 no terceiro quadrado. Este será o momento de manipulação dos alunos até que irá aparecer a seguinte configuração:

Neste momento, acontece a conclusão:
Como a peça 4 tinha área b2 e as peças 1, 2 3 e 5, juntas, tinham área c2 e todas conseguiram completar, sem perda nem sobra de espaço, a área do terceiro quadrado que é a2, então, temos: a2=b2+c2. A mesma informação tinha correspondência ao triângulo retângulo, logo, podemos interpretá-la como: "No triângulo retângulo a medida da hipotenusa ao quadrado é igual à soma dos quadrados dos catetos" - Teorema de Pitágoras.
Assinar:
Postagens (Atom)






