strutura Curricular
PROF : VAGNER MATTOS
EEM PROF MARIETA SANTOS
| MODALIDADE / NÍVEL DE ENSINO | COMPONENTE CURRICULAR | TEMA |
|---|---|---|
| Ensino Fundamental e Médio | Matemática | Espaço e forma |
Dados fhghgAula
O que o aluno poderá aprender com esta aula
O aluno irá vivenciar atividade concreta que envolve o Teorema de Pitágoras.
Duração das atividades
Uma aula de 50 minutos.
Conhecimentos prévios trabalhados pelo professor com o aluno
Triângulos.
Quadrados.
Áreas.
Teorema de Pitágoras.
Quadrados.
Áreas.
Teorema de Pitágoras.
Estratégias e recursos da aula
Objetivo desta aula:O Objetivo desta aula é propor alguns objetos de aprendizagem que permitam um contato diferenciado com o Teorema de Pitágoras. Vale ressaltar que a proposta é diferenciar a dinâmica de aula, isso inclui materiais concretos, objetos virtuais e, também, atividades tradicionais como, por exemplo, a demonstração do Teorema.
Primeira Atividade: Material Concreto
Materiais necessários:
Cada aluno deve ter uma folha com o xerox da seguinte figura:
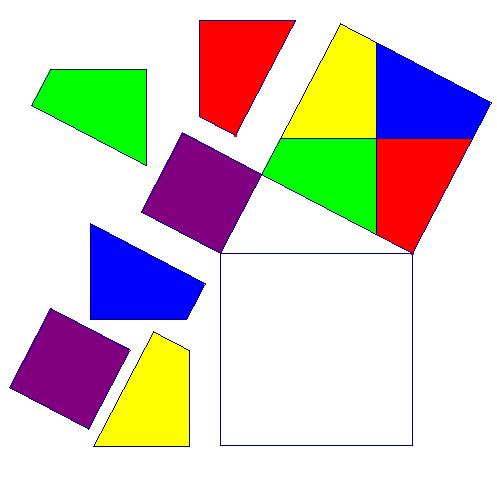
Sugestão:
Imprimir junto, para distribuir aos alunos, uma orientação da atividade:
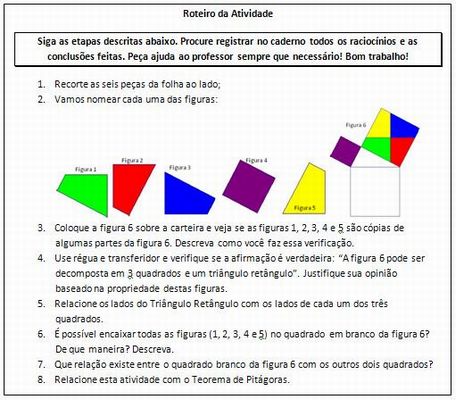
Professor, se este xerox for em preto e branco, verifique se é possível distingüir os diferentes polígonos no xerox. Vale observar que é possível colocar duas destas figuras em cada folha de papel A4. Ou então, uma figura e um roteiro.
Os alunos também devem ter tesoura, régua e transferidor.
Proposta da Atividade:
A vantagem de se usar o material concreto é a possibilidade de sobrepor figuras e observar que elas são congruentes.
Explore, ainda, que:
Neste momento, acontece a conclusão:
Como a peça 4 tinha área b2 e as peças 1, 2 3 e 5, juntas, tinham área c2 e todas conseguiram completar, sem perda nem sobra de espaço, a área do terceiro quadrado que é a2, então, temos: a2=b2+c2. A mesma informação tinha correspondência ao triângulo retângulo, logo, podemos interpretá-la como: "No triângulo retângulo a medida da hipotenusa ao quadrado é igual à soma dos quadrados dos catetos" - Teorema de Pitágoras.
Primeira Atividade: Material Concreto
Materiais necessários:
Cada aluno deve ter uma folha com o xerox da seguinte figura:
Sugestão:
Imprimir junto, para distribuir aos alunos, uma orientação da atividade:

Professor, se este xerox for em preto e branco, verifique se é possível distingüir os diferentes polígonos no xerox. Vale observar que é possível colocar duas destas figuras em cada folha de papel A4. Ou então, uma figura e um roteiro.
Os alunos também devem ter tesoura, régua e transferidor.
Proposta da Atividade:
- Observação da figura: Peça para que os alunos recortem as seis peças da figura. Veja abaixo quais são para orientá-los.

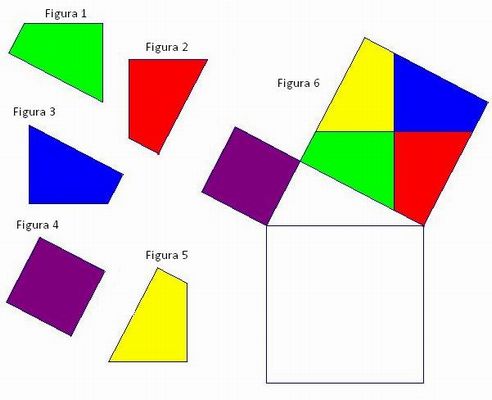
- Interpretação da figura: Os alunos devem fazer uma comparação de áreas das figuras 1, 2, 3, 4 e 5 com a figura 6. O objetivo desta atividade é que eles percebam que o polígono se encaixa (por sobreposição) em uma parte da figura 6 que tenha a mesma cor. Assim, os alunos encontrarão a seguinte figura:

A vantagem de se usar o material concreto é a possibilidade de sobrepor figuras e observar que elas são congruentes.
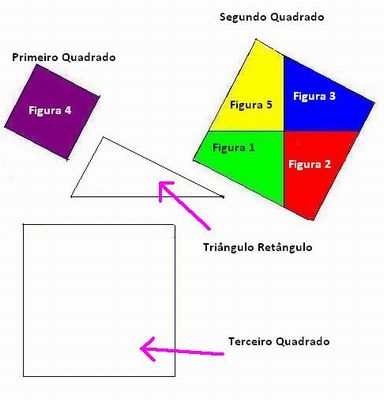
- Conhecendo a figura 6: Utilizando uma régua e transferidor, os alunos podem constatar que a figura 6 é composta de três quadrados (Primeiro quadrado: Figura 4; Segundo quadrado: União das figuras 1,2, 3 e 5; e um Terceiro quadrado que se encontra em branco) e um triângulo retângulo como na figura abaixo:

Explore, ainda, que:
- Existe um lado que é comum ao triângulo retângulo e ao primeiro quadrado. Se chamarmos a medida desta intersecção de "b" podemos concluir que um dos catetos do triângulo retângulo mede "b" e o lado do primeiro quadrado também mede "b". Logo, a área do primeiro quadrado será "b2".
- Também temos um lado que é comum ao triângulo retângulo e ao segundo quadrado. Se chamarmos a medida desta intersecção de "c" podemos concluir que o outro cateto do triângulo retângulo mede "c" e o lado do segundo quadrado também medirá "c". Logo, a área do segundo quadrado será "c2".
- Ainda temos um lado que é comum ao triângulo retângulo e ao terceiro quadrado. Se chamarmos a medida desta intersecção de "a" podemos concluir que a hipotenusa do triângulo retângulo mede " a" e o lado do terceiro quadrado também me de "a". Logo, a área do primeiro quadrado será " a2".
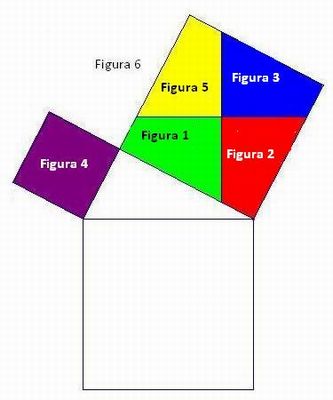
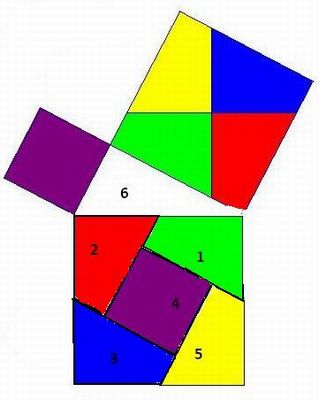
- Conclusão: Após toda esta exploração, é necessário voltar à mesa com as seis figuras novamente separadas. Pergunte aos alunos se é possível encaixar as peças 1, 2, 3, 4 e 5 no terceiro quadrado. Este será o momento de manipulação dos alunos até que irá aparecer a seguinte configuração:

Neste momento, acontece a conclusão:
Como a peça 4 tinha área b2 e as peças 1, 2 3 e 5, juntas, tinham área c2 e todas conseguiram completar, sem perda nem sobra de espaço, a área do terceiro quadrado que é a2, então, temos: a2=b2+c2. A mesma informação tinha correspondência ao triângulo retângulo, logo, podemos interpretá-la como: "No triângulo retângulo a medida da hipotenusa ao quadrado é igual à soma dos quadrados dos catetos" - Teorema de Pitágoras.
Nenhum comentário:
Postar um comentário